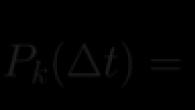Основные элементы СМО

Торговый центр представляет собой однофазную многоканальную систему с одной очередью конечной длины. При заполнении очереди заявка получает отказ. Целью решения задачи моделирования является определение оптимального количества приборов обслуживания, чтобы среднее время пребывания заявки в системе не превышало заданное.

Структуру СМО можно представить таким образом:

Системой массового обслуживания называется система, на которую в случайные моменты времени приходят заявки, нуждающиеся в том или ином виде обслуживания. В данном случае, при моделировании торгового центра роль заявок играют покупатели, а роль приборов продавцы.

Любая система включает в себя 4 основные элемента :

1) входной поток

2) очередь и дисциплины обслуживания

3) прибор и канал обслуживания

4) выходной поток

Входной поток

В процессе функционирования, на вход обслуживающего прибора в неизвестные заранее моменты времени поступают заявки, которые обслуживаются в течение некоторого случайного отрезка времени, после чего прибор освобождается и может принять следующую заявку. Если заявка пришла, когда прибор занят, то она получает отказ в обслуживании и встает в очередь. Из-за случайного характера потока заявок в какие-то моменты времени в системе могут возникать большие очереди, а в другие система может работать с недогрузкой или вообще простаивать. Поэтому возникают задачи количественной оценки эффективности таких систем, обеспечивающих минимизацию суммарных затрат, связанных с ожиданием и потерями со стороны средств обслуживания.

Входной поток может быть одномерным и многомерным. Если на вход системы подается несколько разных потоков, то он является многомерным. Любой входной поток представляется последовательностью однородных событий, следующих одно за другим в случайные моменты времени. Интервал между двумя событиями называется интервалом поступления заявок.

Если интервал поступления заявок является случайной величиной, т.е. изменяется по случайному закону распределения, то поток называется случайным.

Поток называется простейшим или стационарным Пуассоновским потоком, если он обладает 3 свойствами:

1) стационарность

2) безпоследействие

3) ординарность

Стационарность означает, что все вероятностные характеристики потока не зависят от времени. Безпоследействие означает, что события не зависят от предыстории. Ординарность - все заявки проходят по одиночке.

Очередь и дисциплины ее обслуживания

Под очередью понимают линейную цепочку, выстраивающихся в ряд заявок в том или ином виде обслуживания. В зависимости от наличия очереди, СМО разделяются на системы без очереди и системы с ожиданием.

СМО без очереди - это системы, в которых поступившая заявка получает отказ в случае занятости прибора обслуживания.

СМО с ожиданием бывают ограниченными и неограниченными ожиданием. В системах с неограниченным ожиданием поступившая заявка рано или поздно будет обслужена. В системах с ограниченным ожиданием на время пребывания заявок в системе накладывается ряд ограничений, касающихся времени пребывания заявок в очереди, времени пребывания заявок в системе и т.д.

Для регулирования и координации работы очереди используются дисциплины:

1) дисциплина заполнения очереди

2) дисциплина выбора заявок из очереди

К дисциплинам заполнения очереди относятся:

1) естественная форма заполнения

2) кольцевая форма заполнения

3) поисковая форма

4) приоритетная форма заполнения, со сдвигом других заявок

Дисциплины выбора заявок из очереди включают 3 типа:

1) первым пришел - первым обслужен

2) последним пришел - первым обслужен

3) выбор заявок по приоритету

При решении задач управления, в том числе и управления войсками, часто возникает ряд однотипных задач:

• оценка пропускной способности направления связи, железнодорожного узла, госпиталя и т. п.;
• оценка эффективности ремонтной базы;
• определение количества частот для радиосети и др.

Все эти задачи однотипны в том смысле, что в них присутствует массовый спрос на обслуживание. В удовлетворении этого спроса участвует определенная совокупность элементов, образующая систему массового обслуживания (СМО) (рис. 2.9).

Элементами СМО являются:

• входной (входящий) поток требований (заявок) на обслуживание;
• приборы (каналы) обслуживания;
• очередь заявок , ожидающих обслуживания;
• выходной ( выходящий) поток обслуженных заявок;
• поток не обслуженных заявок;
• очередь свободных каналов (для многоканальных СМО).

Входящий поток - это совокупность заявок на обслуживание. Часто заявка отождествляется с ее носителем. Например, поток неисправной радиоаппаратуры, поступающий в мастерскую объединения, представляет собой поток заявок - требований на обслуживание в данной СМО.

Как правило, на практике имеют дело с так называемыми рекуррентными потоками, - потоками, обладающими свойствами:

• стационарности;
• ординарности;
• ограниченного последействия.

Первые два свойства мы определили ранее. Что касается ограниченного последействия, то оно заключается в том, что интервалы между поступающими заявками являются независимыми случайными величинами.

Рекуррентных потоков много. Каждый закон распределения интервалов порождает свой рекуррентный поток . Рекуррентные потоки иначе называют потоками Пальма.

Поток с полным отсутствием последействия, как уже отмечалось, называется стационарным пуассоновским. У него случайные интервалы между заявками имеют экспоненциальное распределение:

здесь - интенсивность потока.

Название потока - пуассоновский - происходит от того, что для этого потока вероятность появления заявок за интервал определяется законом Пуассона:

Поток такого типа, как отмечалось ранее, называют также простейшим. Именно такой поток предполагают проектировщики при разработке СМО. Вызвано это тремя причинами.

Во-первых , поток этого типа в теории массового обслуживания аналогичен нормальному закону распределения в теории вероятностей в том смысле, что к простейшему потоку приводит предельный переход для потока, являющегося суммой потоков с произвольными характеристиками при бесконечном увеличении слагаемых и уменьшении их интенсивности. То есть сумма произвольных независимых (без преобладания) потоков с интенсивностями является простейшим потоком с интенсивностью

Во-вторых , если обслуживающие каналы (приборы) рассчитаны на простейший поток заявок, то обслуживание других типов потоков (с той же интенсивностью) будет обеспечено с не меньшей эффективностью.

В-третьих , именно такой поток определяет марковский процесс в системе и, следовательно, простоту аналитического анализа системы. При других потоках анализ функционирования СМО сложен.

Часто встречаются системы, у которых поток входных заявок зависит от количества заявок, находящихся в обслуживании. Такие СМО называют замкнутыми (иначе - разомкнутыми ). Например, работа мастерской связи объединения может быть представлена моделью замкнутой СМО. Пусть эта мастерская предназначена для обслуживания радиостанций, которых в объединении . Каждая из них имеет интенсивность отказов . Входной поток отказавшей аппаратуры будет иметь интенсивность :

где - количество радиостанций, уже находящихся в мастерской на ремонте.

Заявки могут иметь разные права на начало обслуживания. В этом случае говорят, что заявки неоднородные . Преимущества одних потоков заявок перед другими задаются шкалой приоритетов.

Важной характеристикой входного потока является коэффициент вариации :

где - математическое ожидание длины интервала;

Среднеквадратическое отклонение случайной величины (длины интервала) .

Для простейшего потока

Для большинства реальных потоков .

При поток регулярный, детерминированный.

Коэффициент вариации - характеристика, отражающая степень неравномерности поступления заявок.

Каналы (приборы) обслуживания . В СМО могут быть один или несколько обслуживающих приборов (каналов). Согласно с этим СМО называют одноканальными или многоканальными.

Многоканальные СМО могут состоять из однотипных или разнотипных приборов. Обслуживающими приборами могут быть:

• линии связи;
• мастера ремонтных органов;
• взлетно-посадочные полосы;
• транспортные средства;
• причалы;
• парикмахеры, продавцы и др.

Основная характеристика канала - время обслуживания. Как правило, время обслуживания - величина случайная.

Обычно практики полагают, что время обслуживания имеет экспоненциальный закон распределения:

где - интенсивность обслуживания, ;

Математическое ожидание времени обслуживания.

То есть процесс обслуживания - марковский, а это, как теперь нам известно, дает существенные удобства в аналитическом математическом моделировании.

Кроме экспоненциального встречаются -распределение Эрланга, гиперэкспоненциальное, треугольное и некоторые другие. Это нас не должно смущать, так как показано, что значение критериев эффективности СМО мало зависят от вида закона распределения вероятностей времени обслуживания.

При исследовании СМО выпадает из рассмотрения сущность обслуживания, качество обслуживания .

Каналы могут быть абсолютно надежными , то есть не выходить из строя. Вернее, так может быть принято при исследовании. Каналы могут обладать конечной надежностью . В этом случае модель СМО значительно сложнее.

Очередь заявок . В силу случайного характера потоков заявок и обслуживания пришедшая заявка может застать канал (каналы) занятым обслуживанием предыдущей заявки. В этом случае она либо покинет СМО не обслуженной, либо останется в системе, ожидая начало своего обслуживания. В соответствии с этим различают:

• СМО с отказами;
• СМО с ожиданием.

СМО с ожиданием характеризуются наличием очередей. Очередь может иметь ограниченную или неограниченную емкость: .

Исследователя обычно интересуют такие статистические характеристики, связанные с пребыванием заявок в очереди:

• среднее количество заявок в очереди за интервал исследования;
• среднее время пребывания (ожидания) заявки в очереди. СМО с ограниченной емкостью очереди относят к СМО смешанного типа.

Нередко встречаются СМО, в которых заявки имеют ограниченное время пребывания в очереди независимо от ее емкости. Такие СМО также относят к СМО смешанного типа.

Выходящий поток - это поток обслуженных заявок, покидающих СМО.

Встречаются случаи, когда заявки проходят через несколько СМО: транзитная связь , производственный конвейер и т. п. В этом случае выходящий поток является входящим для следующей СМО. Совокупность последовательно связанных между собой СМО называют многофазными СМО или сетями СМО .

Входящий поток первой СМО, пройдя через последующие СМО, искажается и это затрудняет моделирование . Однако следует иметь в виду, что при простейшем входном потоке и экспоненциальном обслуживании (то есть в марковских системах) выходной поток тоже простейший . Если время обслуживания имеет не экспоненциальное распределение, то выходящий поток не только не простейший, но и не рекуррентный.

Заметим, что интервалы между заявками выходящего потока, это не то же самое, что интервалы обслуживания. Ведь может оказаться, что после окончания очередного обслуживания СМО какое-то время простаивает из-за отсутствия заявок. В этом случае интервал выходящего потока состоит из времени незанятости СМО и интервала обслуживания первой, пришедшей после простоя, заявки.

По характеру входной поток требований разделяется на детерминированный поток требований и стохастический (рис.2).

Детерминированный входной поток может быть двух видов. В первом случае требования поступают через равные промежутки времени. Другим видом детерминированного потока является поток, в котором требования поступают по известной программе - расписанию, когда моменты поступления новых требований известны заранее.

Рис.2. Классификация входного потока

Если промежутки времени между поступлениями требований случайны, то это будет стохастический процесс.

Стохастический поток требований подразделяется на три вида: поток с произвольными стохастическими свойствами, рекуррентный поток и совершенно случайный или пуассоновский поток требований.

Произвольный поток требований характеризуется тем, что на него не накладывается никаких ограничений на стохастическую независимость интервалов между поступлениями требований, а также на характер вероятностных законов, описывающих интервалы между требованиями.

Входной поток называется рекуррентным, если он характеризуется следующими свойствами:

• продолжительность интервалов между поступлениями требований стохастически независимы;
• продолжительность интервалов описывается одной и той же плотностью распределения.

Входной поток называется совершенно случайным или простейшим, если для него характерно:

• продолжительность интервалов между поступлениями требований статистически независимы;
• продолжительность интервалов описывается одной и той же плотностью распределения;
• вероятность поступления требований на достаточно малом интервале Δt зависит только лишь от величины Δt (это свойство называется стационарностью или однородностью прихода);
• вероятность поступления требований на интервале Δt не зависит от предыстории процесса;
• характер потока требований таков, что в любой момент времени может поступить только одно требование.

Таким образом, простейший поток требований или совершенно случайный поток - это поток, определяющейся свойствами стационарности, ординарности и отсутствием последствия одновременно.

Предположения о совершенно случайном входном потоке требований эквивалентно тому, что плотность распределения интервалов времени между последовательными поступлениями требований описывается экспоненциальным законом:

(1.1)

где λ - интенсивность поступления заявок в систему.

Если интервалы распределены по экспоненциальному закону, то процесс пуассоновский. Такие процессы называются М-процессами (Марковскими).

Кроме закона Пуассона часто применяется закон распределения Эрланга.

(1.2)

СМО с отказами

Одноканальная СМО содержит один канал (n = 1), и на ее вход поступает пуассоновский поток заявок П вх интенсивность (среднее число событий в единицу времени) которого inП вх =λ. Так как интенсивность входящего потока может изменяться во времени, то вместо λ записывают λ (t). Тогда время обслуживания каналом одной заявки Т об распределено по показательному закону и записывается в виде: , где λ - интенсивность отказов.

Состояние СМО характеризуется простаиванием или занятостью ее канала, т.е. двумя состояниями: S 0 - канал свободен и простаивает, S 1 - канал занят. Переход системы из состояния S 0 в состояние S 1 осуществляется под воздействием входящего потока заявок П вх, а из состояния S 1 в состояние S 0 систему переводит поток обслуживании П об: если в данный момент времени система находится в некотором состоянии, то с наступлением первого после данного момента времени СМО переходит в другое состояние. Плотности вероятностей перехода из состояния S 0 в S 1 и обратно равны соответственно λ и µ. Граф состояний подобной СМО с двумя возможными состояниями приведен на рис.3.

Рис.3. Граф состояний одноканальной СМО с отказами.

Для многоканальной СМО с отказами (n > 1) при тех же условиях состояния системы обозначим по числу занятых каналов (по числу заявок, находящихся в системе под обслуживанием, так как каждый канал в СМО либо свободен, либо обслуживает только одну заявку).

Таким образом, подобная СМО может находиться в одном из следующих (n+1) состояний: s 0 - все n каналов свободны; s 1 - занят только один из каналов, остальные (n-1) каналов свободны; s i - заняты i - каналов, (n-i) каналов свободны; s n - заняты все n каналов. Граф состояний такой СМО приведен на рис.4.

Рис.4. Граф состояний многоканальной СМО с отказами.

При этом имеет место а

Пользуясь общим правилом составления дифференциальных уравнений Колмогорова, можно для приведенных на рис.2 и рис.3 графов состояний составить системы дифференциальных уравнений:

например, для одноканальной СМО (рис.2) имеем:

для многоканальной СМО (рис.3) соответственно имеем:

Решив первую систему уравнений, можно найти значения p 0 (t) и p 1 (t) для одноканальной СМО и построить графики при трех случаях:

СМО с ожиданием

Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью λ. Интенсивность потока обслуживания равна µ (т.е. в среднем непрерывно занятый канал будет выдавать µ обслуженных заявок). Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N-требований (заявок), т.е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость. Граф состояний СМО в этом случае имеет вид, показанный на рис.6.

Рис.6. Граф состояний одноканальной СМО с ожиданием

Состояния СМО имеют следующую интерпретацию:

S 0 - канал свободен;

S 1 - канал занят (очереди нет);

S 2 - канал занят (одна заявка стоит в очереди);

S n - канал занят (n-1 заявок стоит в очереди);

S N - канал занят (N-1 заявок стоит в очереди).

Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:

(1.11)

где ρ=λ/µ; n - номер состояния.

Решение приведенной выше системы уравнений (1.10) для нашей модели СМО имеет вид:

(1.12)

(1.13)

Следует отметить, что выполнение условия стационарности для данной СМО необязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать N-1), а не соотношением между интенсивностями входного потока, т.е. не отношением λ/µ=ρ. Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной (N-1): вероятность отказа в обслуживании заявки:

(1.14)

относительная пропускная способность системы:

(1.15)

абсолютная пропускная способность:

среднее число находящихся в системе заявок:

(1.17)

среднее время пребывания заявки в системе:

средняя продолжительность пребывания клиента (заявки) в очереди:

(1.19)

среднее число заявок (клиентов) в очереди (длина очереди):

. (1.20) .

Теперь рассмотрим более подробно СМО, имеющую n-каналов с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживаний - интенсивность µ. Необходимо найти предельные вероятности состояний СМО и показатели ей эффективности.

Система может находиться в одном состоянии S 0 , S 1 , S 2 ,…,S k ,…,S n ,…, нумеруемых по числу заявок, находящихся в СМО: S0 - в системе нет заявок (все каналы свободны); S 1 - занят один канал, остальные свободны; S 2 - заняты два канала, остальные свободны; …, S k - занято k каналов, остальные свободны; …, S n - заняты все n каналов (очереди нет); S n +1 - заняты все n каналов, в очереди одна заявка; …, S n + r - заняты все n каналов, r заявок стоит в очереди, ….

среднее число заявок в очереди:

(1.32)

среднее число заявок в системе:

(1.31) .

Элементы теории массового обслуживания

§ 1. Введение

Теория массового обслуживания иначе называется Теория очередей. И действительно, теория массового обслуживания в значительной степени посвящена изучению очередей, возникающих в различных системах.

Основными характеристиками систем массового обслуживания являются следующие случайные величины:

среднее время пребывания клиента в очереди;

доля времени, в течение которого система простаивает (из-за отсутствия клиентов).

Функциональные возможности систем массового обслуживания определяются следующими факторами:

распределение моментов распределения клиентов;

распределение продолжительности обслуживания;

конфигурация обслуживающей системы (последовательное, параллельное или параллельно-последовательное обслуживание);

дисциплина в очереди (обслуживание в порядке поступления, обслуживание в обратном порядке, случайный отбор клиентов);

вместимость блока ожидания (ограниченная или неограниченная);

емкость или мощность источника требования (ограниченная и неограниченная);

некоторые другие характеристики системы (возможности клиентов переходить из одной очереди в другую, ненулевая вероятность отказа и др.).

Основными факторами являются первые два.

Любая система массового обслуживания состоит из следующих основных элементов:

входной поток клиентов;

обслуживающий прибор;

дисциплина в очереди.

§ 2 . Входной поток клиентов

Рассмотрим последовательности случайных величин

Предположим, что t o = 0 – начальный момент функционирования системы; t 1 = t o + τ 1 , t 2 = t 1 + τ 2 , …, t k = t k -1 + τ k , …., где τ k – независимые случайные величины, имеющие показательное распределение с параметром λ.

Здесь t 1 – момент поступления первого клиента, τ 1 – промежуток времени между началом работы системы и моментов прихода первого клиента, τ 2 – промежуток времени между моментами прихода первого и второго клиентов, и т.д.

Последовательность
, заданная вышеуказанным образом называется простейшим (пуассоновским ) потоком . А постоянная называется параметром простейшего потока.

Свойства простейшего потока

1. Сдвиг потока на величину Т

Пусть имеется простейший поток
с параметром λ.

Сдвигая поток на величину Т , получаем поток
, который также будет являться простейшим потоком с тем же параметром λ. Например, если T находится между и , то новый поток выглядит так:

, ….

2. Слияние двух потоков

П
усть имеются два независимых простейших потока

с
параметрами λ (1) , λ (2) соответственно. Будем говорить, что поток образовался в результате слияния двух потоков, если множество {t k } есть объединение множеств {t k (1) }, {t k ( 2) } и элементы множества {t k } упорядочены в порядке возрастания.

П
оток, получившийся в результате слияния двух независимых простейших потоков, является тоже простейшим потоком с параметром λ = λ (1) + λ (2) , где λ (j) – параметр потока

3. Разделение простейшего потока

Пусть имеется простейший поток с параметром λ,

и последовательность независимых случайных величин
, принимающих два значения:

P(ξ i = 1) = p , P(ξ i = 0) = q , p  0, q  0, p + q = 1.

Такие случайные величины называются бернуллиевскими (с параметром p ). Процедура разделения потока {t k } состоит в следующем: число t i отнесем к первому потоку, если ξ i = 1; если же ξ i = 0, то число t i отнесем ко второму потоку. Такую операцию разделения потока на два назовем бернуллиевской (с параметром p ).

Потоки, полученные в результате бернуллиевского разделения простейшего потока, являются независимыми простейшими потоками с параметрами λ (1) = λp, λ (2) = λq соответственно.

Отметим, что доказательства этих свойств простейшего потока можно найти в .

Ч
ерез X(t) в дальнейшем будем обозначать число клиентов в системе в момент t , т.е.

Свойства пуассоновских процессов

Приращение пуассоновского процесса однородное .

Обозначим через X ((a ,b ]) = X (b ) – X (a ) приращение процесса, которое может быть интерпретировано как число клиентов, поступающих в систему в промежутке (a ,b ]. Однородность означает выполнение условия:

P(X ((a ,b ]) = k) = P(X ((0,b -a ]) = k) = P(X (b -a ) = k),

т.е. распределение вероятностей числа клиентов, поступающих в систему в промежутке (a ,b ], зависит только от длины этого промежутка.

Приращения пуассоновского процесса независимы .

Рассмотрим промежуток (0, b ] и предположим, что он разбит на непересекающиеся промежутки (0, b 1 ], (b 1 , b 2 ], , (b N -1 , b N ]. Пусть b 0 = 0. Тогда X ((b 0 , b 1 ]), X ((b 1 , b 2 ]), , X ((b N -1 , b N ]) – число клиентов, поступающих в систему в соответствующие периоды времени. Эти величины независимы, т.е.

P(X ((b 0 , b 1 ]) = i 1 , , X ((b N -1 , b N ]) = i N) =

P(X ((b 0 , b 1 ]) = i 1)  P(X ((b N-1 , b N ]) = i N).

Доказательства этих свойств можно найти в .

Задачи к § 2.

2.1. Имеются две случайные величины  1 и  2 . Они независимые и имеют показательное распределение с параметрами  1 и  2 соответственно. Введем следующую случайную величину:  = min{ 1 ,  2 }. Доказать, что эта величина имеет показательное распределение с параметром = 1 + 2 .

2.2. Даны две независимые случайные величины  1 и  2 , имеющие пуассоновское распределение с параметром  1 и  2 соответственно. Пусть случайная величина  = 1 + 2 . Доказать, что эта величина имеет распределение Пуассона с параметром  = 1 + 2 .

2.3. Пусть  - число клиентов в магазинах и имеет распределение Пуассона с параметром  . Пусть каждый клиент с вероятностью p делает покупку в этом магазине. Требуется доказать, что число клиентов, сделавших покупку в этом магазине, имеет распределение Пуассона с параметром p .

2.4. Посетители приходят в ресторан в соответствии с пуассоновским потоком со средней частотой 20 посетителей в час. Ресторан открывается в 11.00.

а) вероятность того, что в 11.12 в ресторане окажется 20 посетителей при условии, что в 11.07 в ресторане было 18 посетителей;

б) вероятность того, что новый посетитель прибудет в ресторан в интервале между 11.28 и 11.30, если известно, что предыдущий посетитель прибыл в ресторан в 11.25.

2.5. Продукция берется со склада, вмещающего 80 единиц складируемой продукции, в соответствии с пуассоновским потоком с интенсивностью 5 единиц продукции вдень.

а) вероятность того, что в течении первых двух дней со склада будет взято 10 единиц продукции;

б) вероятность того, что к концу четвертого дня на складе не останется ни одной единицы продукции.

§

3. Процесс гибели и размножения

Построим процесс гибели и размножения X (t ) «конструктивно».

Рассмотрим две последовательности и. Первая - отвечает за поступление клиентов в систему (размножение), а вторая - за обслуживание клиентов (гибель):

Кроме того, пусть заданы две независимые последовательности
независимых случайных величин с показательным распределением с параметром =1.

Процесс X (t) строится так. Пусть
, где
. Тогда на интервале
процесс X (t) сохранит свое значение , где
,

.

В момент t 1 значение процесса X (t ) либо увеличится, либо уменьшится на единицу в соответствии с тем, какой из двух моментов
наступит раньше:

Мы положили, таким образом, значение процесса X (t) в точке t 1 равным ; тогда эволюция процесса X (t ) на интервале
, где
и
, подчиняется тому же закону закону: X (t ) не меняется на этом интервале в момент t 2

увеличивается на единицу, если
, и уменьшается на единицу в противном случае.

Если же
, то значение процесса X (t ) увеличивается на единицу в случайный момент
.

Построенный таким образом процесс
, называется однородным по времени процессом гибели и размножения; его распределения полностью определяются набором параметров, и начальным распределением X(0):

Удобно использовать следующую диаграмму для представления развития процесса X (t):

Стрелочки сверху соответствуют динамике процесса размножения: из i -го состояния процесс переходит в (i +1)-е состояние с интенсивностью ; стрелочки снизу соответсвуют динамике процесса гибели: с интенсивностью процесс из i -го состояния переходит в (i -1)-е состояние.

Набор функций

описывает распределение процесса X (t ); ниже мы приведем систему уравнений, которым удовлетворяют эти функции.

Отметим, что не всякому набору параметров
отвечает «невырожденный» процесс X (t ); дело в том, что если числа растут очень быстро при
, то процесс X (t ) в конечный момент t может «взорваться», т.е. с положительной вероятностью превысить любой уровень и возрасти до
. Так ведут себя, например, популяция бактерий в благоприятной среде. Аналогично устроены процессы, описывающие химические реакции, приводящие к взрыву.

Процессы X (t ), для которых все
, относятся к так называемым процессам чистого размножения . Процессы, для которых
, называют процессами чистой гибели .

Следующая лемма дает необходимые и достаточные условия на параметры
, которые гарантируют конечность процесса чистого размножения
с параметрами .

Лемма . Пусть процесс чистого размножения с параметрами . Тогда для конечности процесса необходимо и достаточно, чтобы расходился ряд

Пусть X (t ) процесс гибели и размножения с теми же параметрами процесса , а также параметрами
. Очевидно, что

P(X (t )  )  P(X + (t )  ) .

Поэтому из леммы получаем следствие.

Следствие . Если для произвольного процесса гибели размножения X(t) выполнено условие
, то для любого
справедливо P(X(t)  ) = 1, т.е. процесс конечен.

Доказательство леммы можно найти в .

Задачи к § 3

3.1. Рассмотрим процесс гибели и размножения, для которого

Требуется изобразить диаграмму, отвечающую этому процессу.

3.2. Пусть клиенты, которые хотят получить справку по телефону, образуют простейший поток с параметром . Пусть каждый разговор длится -показательное время. Пусть X (t ) – число клиентов в системе в момент t. Изобразить диаграмму, отвечающую процессу X (t ).

3.3. Пусть в условиях задачи 3.2

телефон имеет память на одного клиента: если клиент звонит и телефон занят, но память телефона свободна, то автомат предлагает положить трубку и ждать звонка. Когда телефон освободится, звонок прозвучит;

имеется автоматический коммутатор и два телефона, у каждого телефона свой оператор: если в момент звонка клиента имеется свободный телефон, то коммутатор автоматически адресует клиента на этот телефон;

коммутатор (см п.2)) имеет память на одного клиента;

каждый телефон (см.п.2)) имеет память на одного клиента.

Для всех вышеперечисленных случаев изобразить диаграмму, отвечающему процессу X (t ).

3.4. Установить, являются ли конечными процессы чистого размножения со следующими интенсивностями размножения:

а)  k =k  +  ,  >0,  >0, k = 0, 1, ...

б)  0 = 1,  k +1 = (k +1) k , k = 0, 1, ...

в)  k =  k , k = 0, 1, ...  > 0.

§ 4. Дифференциальные уравнения, отвечающие процессу гибели и размножения

Предположим, что X (t ) – процесс гибели и размножения с характеристиками и. Пусть для некоторых конечных чисел A и B имеют место неравенства  i  A + Bi , i = 0, 1, ...Это условие гарантирует конечность процесса X (t ). При этом мы условимся, что в каждое состояние приходит верхняя стрелочка слева (даже в состояние 0), при этом интенсивность рождения λ может равняться нулю (например, λ –1 = = 0); из каждого состояния выходит нижняя стрелочка влево, и интенсивность гибели μ тоже может равняться нулю (например, λ –1 = 0). Доопределение таким образом диаграммы не меняет суть дела, однако в дальнейших рассуждениях будет полезно. Рассмотрим диаграмму, отвечающую нашему процессу X (t ):

Обозначим, как и ранее, через

P k (t ) = P (Х (t ) = k ), k = 0,1,…,

вероятности того, что в фиксированный момент t число клиентов X (t ) будет равно k.

Теорема 1. Характеристики процесса X (t ), определенное выше, удовлетворяет следующей системе дифференциальных уравнений

где k = 0,1,…, и начальным условиям

Нелишне пояснить, что первая строка (при k = 0) системы уравнений (1) имеет вид

Доказательство. Обозначим через P k (t + Δ) = P (X (t + Δ) = k ).

Воспользуемся определением производной функции одной переменной:

.

Рассмотрим такие события:

A 0 (t , Δ) = {на отрезке [t , t +Δ] процесс X (t ) не совершил ни одного скачка};

A 1 (t , Δ) = {на отрезке [t , t +Δ] процесс X (t ) совершил ровно один скачок};

A 2 (t , Δ) = {на отрезке [t , t +Δ] процесс X (t ) совершил два скачка и более}.

Тогда очевидно, что

Обозначим далее через

; через
три показательные случайные величины с параметрами
. Пусть все эти величины независимы. Тогда верно Тогда очевидно, чтостационарном (установившемся) режиме. P k (t ) = P (в системе в момент t находится k клиентов).

Найдите решение системы дифференциальных уравнений, а также стационарные вероятности.

4.2. Для процессов гибели и размножения из задачи 3.3 выписать дифференциальные уравнения, связывающие вероятности P k (t ) = P (в системе в момент t находится k клиентов).

Найти стационарные вероятности.

Основная задача ТСМО заключается в установлении зависимости между характером потока заявок на входе СМО, производительностью одного канала, числом каналов и эффективностью обслуживания.

В качестве критерия эффективности могут быть использованы различные функции и величины:

• среднее время простоя системы;
• среднее время ожидания в очереди;
• закон распределения длительности ожидания требования в очереди;
• средний % заявок, получивших отказ; и т.д.

Выбор критерия зависит от вида системы. Например, для систем с отказами главной характеристикой является абсолютная пропускная способность СМО; менее важные критерии - число занятых каналов, среднее относительное время простоя одного канала и системы в целом. Для систем без потерь (с неограниченным ожиданием) важнейшим является среднее время простоя в очереди, среднее число требований в очереди, среднее время пребывания требований в системе, коэффициент простоя и коэффициент загрузки обслуживающей системы.

Современная ТСМО является совокупностью аналитических методов исследования перечисленных разновидностей СМО. В дальнейшем из всех достаточно сложных и интересных методов решения задач массового обслуживания будут изложены методы, описываемые в классе марковских процессов типа “гибель и размножение”. Это объясняется тем, что именно эти методы чаще всего используются в практике инженерных расчетов.

2. Математические модели потоков событий.

2.1. Регулярный и случайный потоки.

Одним из центральных вопросов организации СМО является выяснение закономерностей, которым подчиняются моменты поступления в систему требований на обслуживание. Рассмотрим наиболее употребляемые математические модели входных потоков.

Определение: Поток требований называют однородным, если он удовлетворяет условиям:

1. все заявки потока с точки зрения обслуживания являются равноправными;

вместо требований (событий) потока, которые по своей природе могут быть различными, рассматриваются толь ко моменты их поступления.

Определение: Регулярным называются поток, если события в потоке следуют один за другим через строгие интервалы времени.

Функция f (х) плотности распределения вероятности случайной величины Т – интервала времени между событиями имеет при этом вид:

Где - дельта функция, М т - математическое ожидание, причем М т =Т, дисперсия D т =0 и интенсивность наступления событий в поток =1/M т =1/T.

Определение: Поток называют случайным , если его события происходят в случайные моменты времени.

Случайный поток может быть описан как случайный вектор, который, как известно, может быть задан однозначно законом распределения двумя способами:

Где, zi - значения Ti(i=1,n), В этом случае моменты наступления событий могут быть вычислены следующим образом

t 1 =t 0 +z1

t 2 =t 1 +z2

………,

где, t 0 - момент начала потока.

2.2. Простейший пуассоновский поток.

Для решения большого числа прикладных задач бывает достаточным применить математические модели однородных потоков, удовлетворяющих требованиям стационарности, без последействия и ординарности.

Определение: Поток называется стационарным, если вероятность появления n событий на интервале времени (t,t+T) зависит от его расположения на временной оси t.

Определение: Поток событий называется ординарным, если вероятность появления двух или более событий в течении элементарного интервала времени D t есть величина бесконечно малая по сравнению с вероятностью появления одного события на этом интервале, т.е. при n=2,3,…

Определение: Поток событий называетсяпотоком без последствия , если для любых непересекающихся интервалов времени число событий, попадающих на один из них, не зависит от числа событий попадающих на другой.

Определение: Если поток удовлетворяет требованиям стационарности, ординарности и без последствия он называется простейшим, пуассоновским потоком.

Доказано, что для простейшего потока число n событий попадающих на любой интервал z распределено по закону Пуассона:

(1)

Вероятность того, что на интервале времени z не появится ни одного события равна:

(2)

тогда вероятность противоположного события:

где по определению P(T это функция распределения вероятности Т. Отсюда получим, что случайная величина Т распределена по показательному закону:

(3)

параметр называют плотностью потока. Причем,

Впервые описание модели простейшего потока появились в работах выдающихся физиков начала века – А. Эйнштейна и Ю.Смолуховского, посвященных броуновскому движению.

2.3. Свойства простейшего пуассоновского потока.

Известны два свойства простейшего потока, которые могут быть использованы при решении практических задач.

2.3.1. Введем величину a= х. В соответствии со свойствами Пуассоновского распределения при оно стремится к нормальному. Поэтому для больших а для вычисления Р{Х(а)меньше, либо равно n}, где Х(а) – случайная величина распределенная по Пуассону с матожиданием а можно воспользоваться следующим приближенным равенством:

2.3.2. Еще одно свойство простейшего потока связано со следующей теоремой:

Теорема: При показательном распределении интервала времени между требованиями Т, независимо от того, сколько он длился, оставшаяся его часть имеет тот же закон распределения.

Доказательство: пусть Т распределено по показательному закону: Предположим, что промежуток а уже длился некоторое время а< Т. Найдем условный закон распределения оставшейся части промежутка Т 1 =Т-а

F a (x)=P(T-ax)

По теореме умножения вероятностей:

P((T>a)(T-az) P(T-aa)=P(T>a) F a (z).

Отсюда,

равносильно событию а, для которого P(а; с другой стороны

P(T>a)=1-F(a), таким образом

F a (x)=(F(z+a)-F(a))/(1-F(a))

Отсюда, учитывая (3):

Этим свойством обладает только один вид потоков – простейшие пуассоновские.